Effects of an Internal Constraint in Flow-Based Welfare Maximization

Bengt J. Olsson
LinkedIn: beos
X/Twitter: @bengtxyz 

The three-zone market model with flow-based constraints is a simple, yet non-trivial, framework for analysing how network constraints affect welfare maximization — and consequently prices, flows, and congestion income.

It describes a market with three connected zones, where one zone also has an internal congestion. All zones have the same demand, but the production cost in Zone 0 is higher than in Zone 1 that is higher than in Zone 2. Thus economically, power flows should be directed towards Zone 0. While this is also the case as seen in the referred model, the physical properties constrains the flow to differ from the purely economical flow.

In this post, we revisit the same three-zone system introduced earlier, now focusing on the effects of a single internal constraint located in Zone 1. In the previous blog behavior for RAM values of 4 and 2 where studied in detail. Here we look at the propoerties when we “continuosly” varies RAM.

Readers unfamiliar with the model setup are encouraged to consult the earlier blog post for background and definitions.

Model setup

All inter-zonal border links are kept effectively unconstrained by assigning them a high capacity value (C = 100). The only active limitation in the system is the internal constraint in Zone 1, whose available capacity (RAM) is varied.

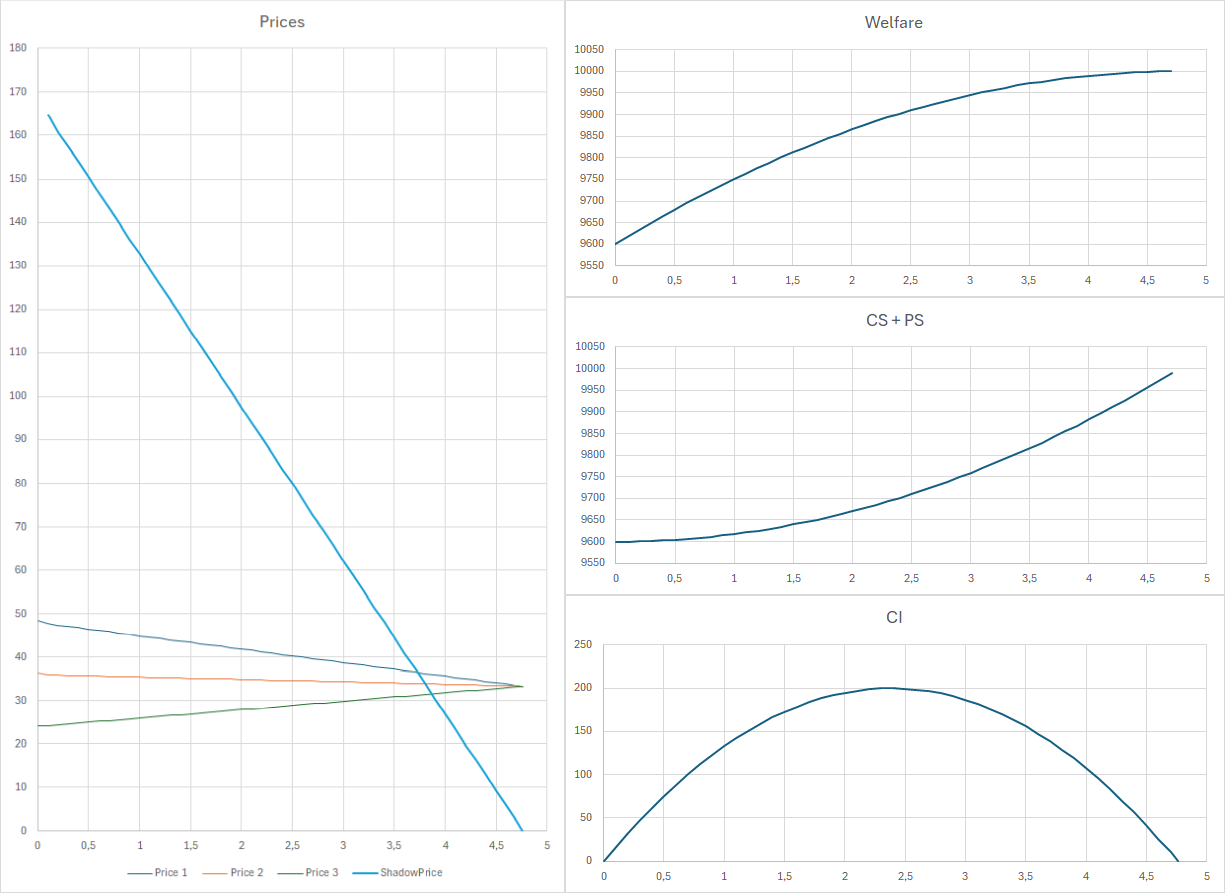
RAM is increased from zero in steps of 0.1, up to the point where the constraint ceases to be binding. This occurs at:

RAM = 4.762

For RAM values above 4.762, the system is effectively unconstrained, and power can flow freely in a way that maximizes total system welfare.

Reference case: unconstrained system

From the earlier blog post, the unconstrained equilibrium is:

• Total welfare W = 10 000
• Consumer surplus CS = 6 666.7
• Producer surplus PS = 3 333.3
• Congestion income CI = 0
• Zonal prices equalized to 33.33

These values serve as a reference throughout the discussion.

RAM = 0: fully binding internal constraint

Starting from RAM = 0, total welfare is approximately:

W = 9 600

This is 400 below the unconstrained benchmark.

At RAM = 0:

• There is no flow over the internal constraint
• Congestion income CI is zero
• Zonal prices differ substantially
• The shadow price λ of the constraint is undefined

Here, the shadow price is inferred “backwards” (since CI = ∑_c(λ_c*RAM_c) and here there is only one constraint) as:

λ = CI / RAM

Since both CI and RAM are zero, λ is undefined here — not sure what it would be in formal theory, it seems to converge to 168 for very small values of RAM.

It is quite interesting that when RAM = 0, CI becomes zero, but we still have flows between zones with price differences. The only logical conclusion is thus that CI emerging from different border flows cancels. And this is exactly what happens. Links between Zone 0 and Zone 1, and between Zone 1 and Zone 2 gets a CI value of 48 and -48 respectively, while flow from Zone 2 to Zone 0 is zero and consequently its CI is zero.

Increasing RAM: marginal effects

When RAM is increased to 0.1, several effects appear immediately:

• The shadow price λ of the internal constraint is approximately 165
• Total welfare increases with a slope of about 165 (since dW/dRAM = λ)
• Both CI and CS + PS increase
• Initially, CI increases faster than CS + PS

As RAM continues to increase, congestion income rises and reaches a maximum of 200 at:

RAM ≈ 2.4

Beyond this point, CI begins to decline and eventually reaches zero when the constraint is no longer binding and zonal prices converge. As noted earlier, this occurs at RAM = 4.762.

Insight — how CS + PS responds to increasing RAM

For a single binding constraint:
CI(RAM) = λ(RAM) × RAM

Total welfare can be written as:
W = CS + PS + CI

Taking derivatives with respect to RAM gives:
d(CS + PS)/dRAM
= dW/dRAM − dCI/dRAM
= λ − (λ + RAM × dλ/dRAM)

which simplifies to:
d(CS + PS)/dRAM = − RAM × dλ/dRAM

Since the shadow price λ is a non-increasing function of RAM, this derivative is always non-negative.

Key observations

Several important insights can be drawn from this experiment:

• Diminishing marginal welfare gains
  Increasing RAM yields larger welfare improvements at low RAM than at high RAM — a direct analogue of diminishing marginal utility.
  • This is also seen on the negative slope of the shadow price. The shadow price is by definition the marginal utility from RAM.
• At low RAM, welfare gains mainly appear as congestion income
  When the constraint is very tight, most of the welfare gain initially materializes as CI, while CS + PS grows more slowly.
• At higher RAM, welfare gains shift toward CS + PS
  As the shadow price falls, a larger share of the additional welfare accrues directly to consumers and producers.
  • Compare with zonal price differences that are larger the tighter the constraint is.
    Relaxing the constraints => smaller price differences => less CI
• CS + PS increases monotonically with RAM
  Regardless of how CI behaves, the combined consumer and producer surplus always increases as the constraint is relaxed.

Key result

Because the shadow price λ is non-increasing in RAM, relaxing a binding constraint always increases CS + PS. Congestion income may rise initially and later fall, but the consumer–producer collective always benefits from easing the constraint.

Interpretation

The last observation is particularly important.

Independent of how welfare is distributed between congestion income and market participants, relaxing a binding network constraint always benefits the consumer–producer collective.

Congestion income is therefore not an objective in itself, but a consequence of scarcity. As capacity expands, scarcity rents eventually disappear, while total welfare — and especially CS + PS — continues to increase.

Takeaway

Congestion income is not something the market tries to maximize. It is the shadow value of scarce network capacity. Expanding capacity always increases total welfare and CS + PS, even though congestion income may temporarily rise or fall.

---

Appendix

For this particular three-zone system, the welfare maximization problem admits an analytical solution. Total welfare can be written explicitly as a function of the available capacity (RAM) of the internal constraint, for RAM values between 0 and 4.762:

W(RAM) = 9 600 + 168 × RAM − (168 / (2 × 4.762)) × RAM²

This concave quadratic form reflects diminishing marginal welfare gains as RAM increases.

Shadow price as the marginal value of RAM

The shadow price λ of the internal constraint is given by the derivative of welfare with respect to RAM:

λ = dW/dRAM
λ = 168 × (1 − RAM / 4.762)

Thus, λ is a linear function of RAM with a negative slope. This matches exactly the straight, downward-sloping shadow price curve observed in the numerical results.

At RAM = 0, the constraint is extremely tight and the marginal value of relaxing it is high. As RAM increases, scarcity is gradually reduced and the shadow price declines linearly, eventually reaching zero when the constraint is no longer binding.

Congestion income and its maximum

Congestion income is given by:

CI = λ × RAM
CI = 168 × (1 − RAM / 4.762) × RAM

This expression makes clear that congestion income is the product of two opposing effects:

• RAM increases linearly
• λ decreases linearly

Differentiating CI with respect to RAM gives:

dCI/dRAM = 0 at RAM = 4.762 / 2

Thus, congestion income reaches its maximum exactly halfway to the point where the constraint ceases to be binding. At this point, CI is approximately 200, consistent with the numerical results.

Consumer and producer surplus

Consumer plus producer surplus is obtained as the residual:

CS + PS = W − CI
CS + PS = 9 600 + (168 / (2 × 4.762)) × RAM²

This expression shows that CS + PS increases monotonically and convexly with RAM. While congestion income may rise and fall, the combined surplus of consumers and producers always increases as the constraint is relaxed.

Implications for prices

The zonal price difference is proportional to the shadow price λ. Since λ is linear in RAM, zonal prices also vary linearly with RAM in this model.

This explains the linear price trajectories observed in the numerical simulations and highlights the tight link between scarcity (λ), price separation, and congestion income in the flow-based welfare-maximizing framework.

Interpretation

This analytical solution neatly ties together all key observations:

• Welfare is concave in RAM
• The shadow price is linear and decreasing
• Congestion income is non-monotonic and peaks at intermediate RAM
• CS + PS increases monotonically
• Zonal price differences decline linearly as capacity expands

---