Bengt J. Olsson
X: @bengtxyz
LinkedIn: beos
Aleksei Seleznev från Montel gör en riktigt intressant analys av flödena mellan SE2-SE3-SE4 i den här LinkedIn posten. I den kan man observera att SE3 priset påfallande ofta är ganska exakt lika med medelvärdet mellan priset av SE2 och SE4. Hur ska man förklara detta? Det är ganska intrikata orsakssamband, men genom att modellera priser med den här förenklade prismarknadsmodellen kan man få en viss förståelse för marknadsdynamiken, och dess bakomliggande fysikaliska orsaker.
Först lite statistik: mellan Januari och Maj i år, 2025, så var kvoten mellan medelvärdet av SE2+SE4 priset och SE3 priset mellan 0.9 och 1.1 ganska precis 50% av timmarna, och mellan 0.99-1.01 14% av timmarna. Övrig tid är kvoten spridd ganska jämnt mellan 0.5 och 1, och med några utstickare över 1. Distributionen är plottad i histogrammet nedan, vänstra figuren. Högra figuren innehåller en simulering med min modell men vi återkommer till den.
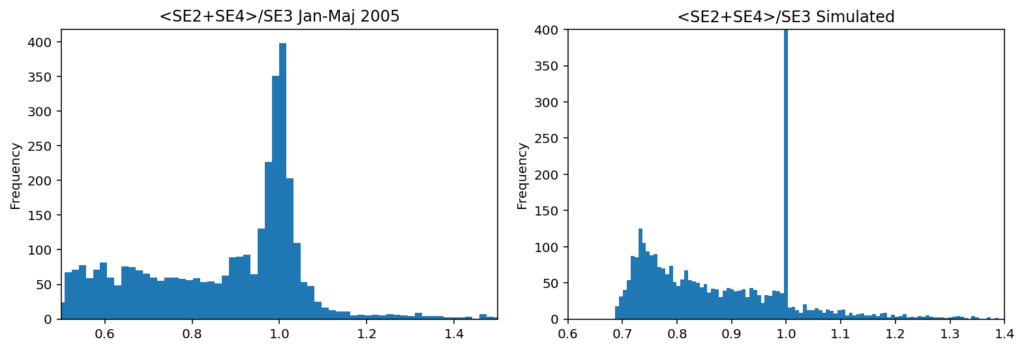
Det finns alltså en stark koncentration med timmar där priskvoten ligger nära 1. Hur ska man förklara detta? Om vi utgår från Alekseis hypotes så kan vi modellera flödet i SE2, SE3 och SE4 med följande starkt förenklade modell.
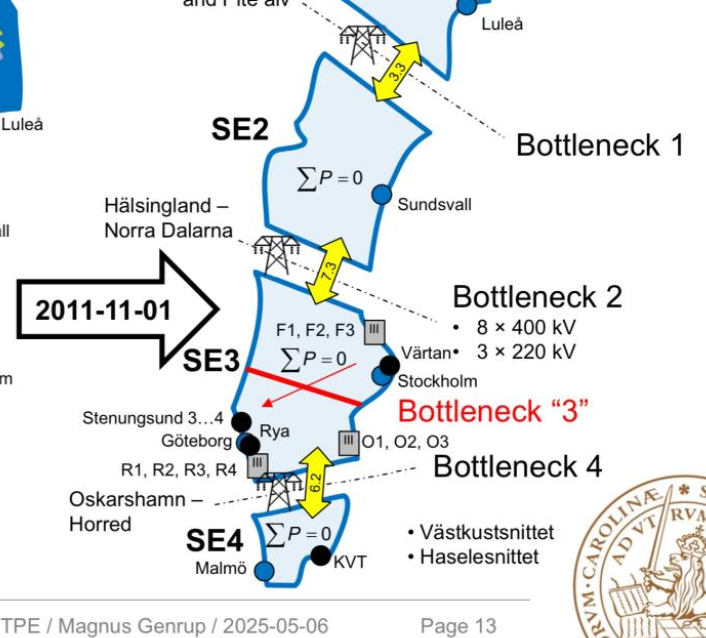
Vi antar att SE2 och SE3 förbinds via en länk L23 och SE3, SE4 via L34. Men internt i SE3 har vi också en flaskhals som kan vara, men inte behöver vara, begränsande. Låt oss modellera den som en länk Lab, där “a” står för ett fiktivt elområde SE3a i östra Svealand och “b” för SE3b i västra Svealand. Magnus Genrup på LTH illusterar detta i figuren nedan, där Bottleneck “3” motsvarar vår Lab. I den här modellen är SE3a och SE3b “ekvivalenta”, dvs de har liknande produktions/konsumtionskapacitet. Kan förklaras av att SE3a har Forsmark och Fenno-Scan länken, medan SE3b har Ringhals och Oskarshamn. Detta är viktigt för de sk “generation shift factors (GSK)” som visar med hur respektive halva bidrar till SE3s nettoposition.
Hur dessa tre länkar och områden är hopkopplade flödesmässigt kan väldigt förenklat beskrivas med en PTDF matris som bestämmer flödena över länkarna som en funktion av respektive elområdes nettoposition:
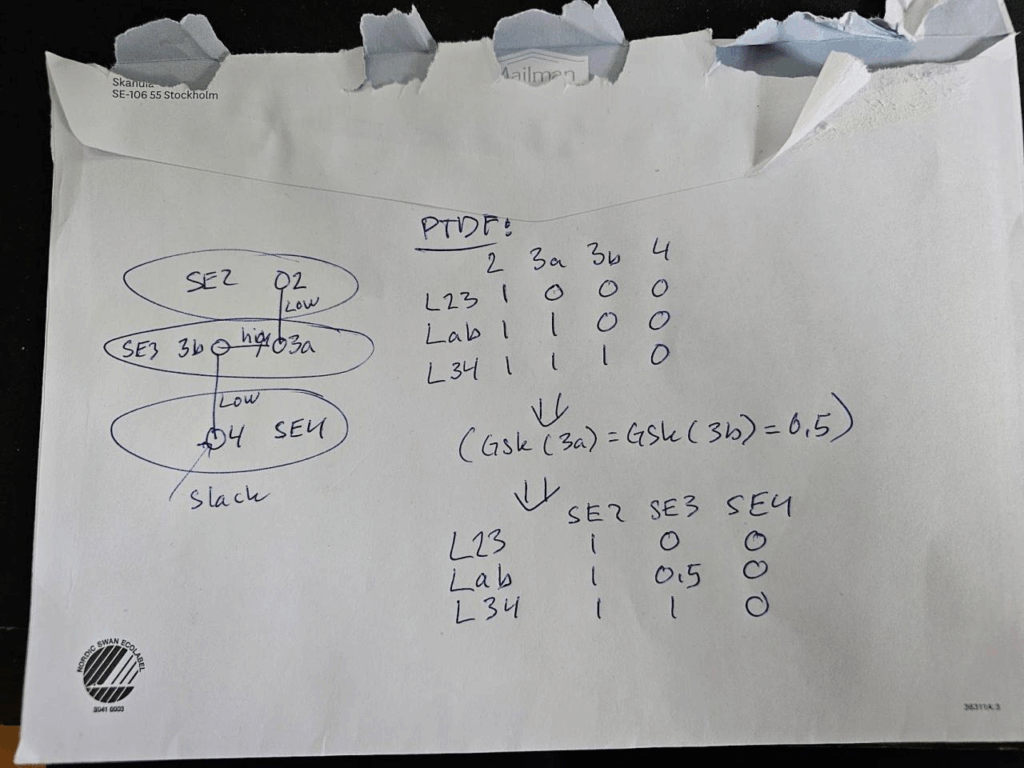
Om t ex ytterligare en MW tillförs i (hela) SE3, och ska tas ut i SE4 kommer en halv MW belasta den interna flaskhalsen, och en hel MW flödar över till SE4. Detta för att hälften (GSK = 0.5) av den tillförda effekten skapas is SE3a och den andra hälften i SE3b. Detta är inte så konstigt. Men nu kommer det kluriga: Från optimeringsteori vet vi att när en begränsning i nätet (CNEC) är aktiv har den ett skuggpris μ, som anger hur mycket det är värt att öka kapaciteten i den med 1 MW. Om ett område i’s nettoposition ändras med +1 MW, belastas flaskhalsen enligt PTDFi. Skillnaden i PTDF mellan två områden bestämmer hur deras priser skiljer sig åt:
Pi−Pj=μ⋅(PTDFj−PTDFi).
I vårt exempel har vi PTDF(SE2)=1, PTDF(SE3)=0.5, PTDF(SE4)=0. Därför blir SE4 μ €/MWh dyrare än SE2, och SE3 hamnar 0.5 μ €/MWh över SE4.
SE3-priset ligger alltså mitt emellan SE2 och SE4, just därför att dess PTDF ligger mitt emellan deras.
I figuren nedan så är alltså skuggpriset μ, givet modellen 84 EUR/MWh. SE3 priset 50 = (92+8)/2. Enligt Aleksei ligger skuggpriset i medel under året hittils på ca 56 EUR/MWh så priset blir typiskt 28 EUR/MWh dyrare i SE4 än i SE3 när begränsningen är aktiv (och motsvarande 28 EUR/MWh dyrare i SE3 än i SE2).
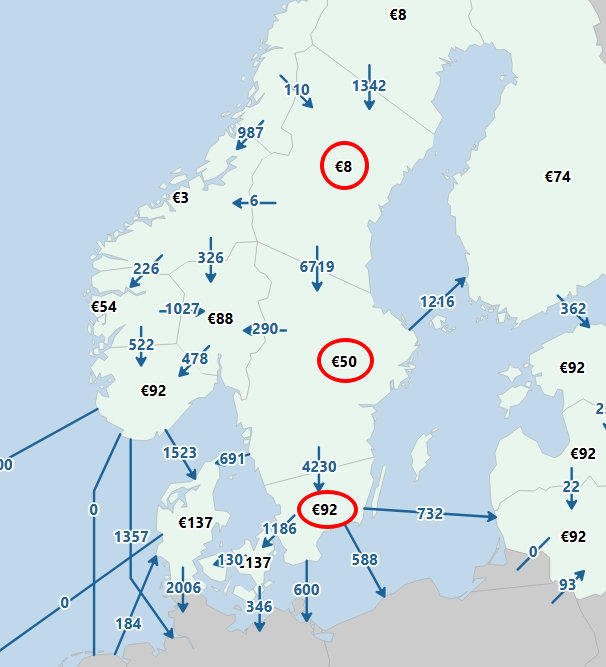
Hela analysen bygger på att länkarna som förbinder de “riktiga” elprisområdena, L23 och L34 inte är begränsande. I fall de också är det så får ju dessa också ett skuggpris som adderar till prisskillnaden. Men det som vi ser hända i simuleringarna är att, i många fall, när begränsningen Lab är aktiv så minskar det flödet på länkarna L23 och L34, och då blir priskvoten exakt 1.
Och omvänt, om vi inte har någon begränsning av flaskhalsen Lab så blir i stället, i allmänhet, L23 och L34 begränsande. L23 mer begränsande än L34 så prisskillnaden mellan SE2 och SE3 blir större än mellan SE3 och SE4. Det är detta som avspeglas i den mer “kontinuerliga” fördelningen av kvot-värden som ligger mellan 0.5 och 1 i grafen oven.
Min modell som som modellerar tre kopplade elprisområden med bara linjära utbuds och efterfrågekurvor ser priserna ut som nedan, till vänster utan flaskhals och till höger med flaskhals i SE3
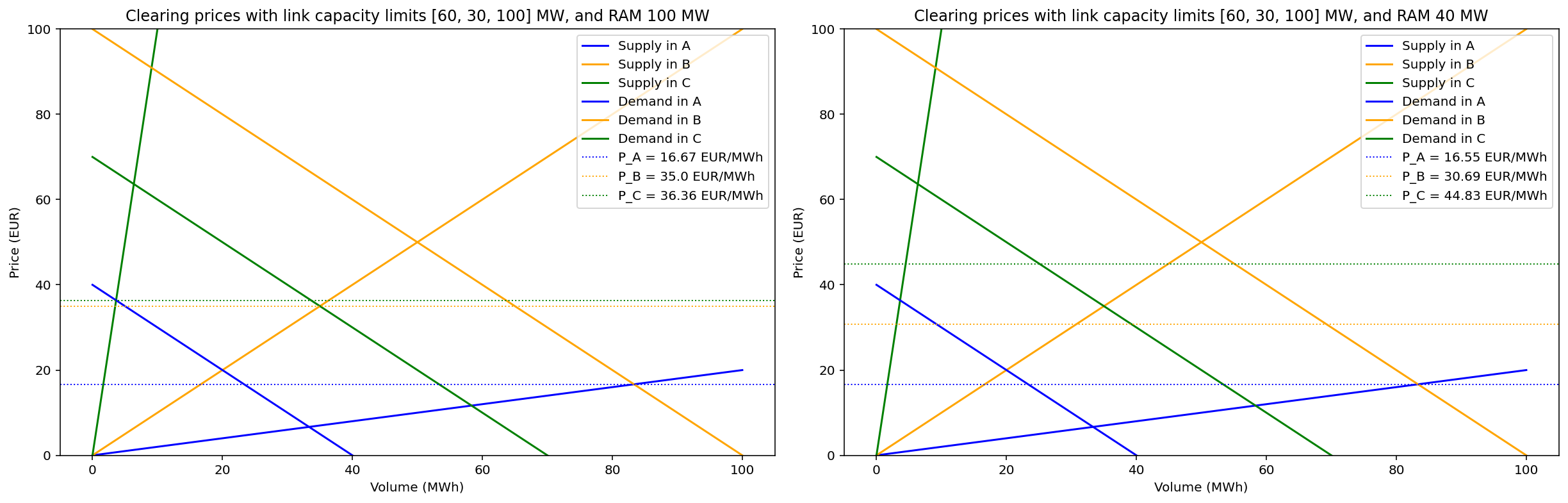
Motsvarande data från simuleringarna:
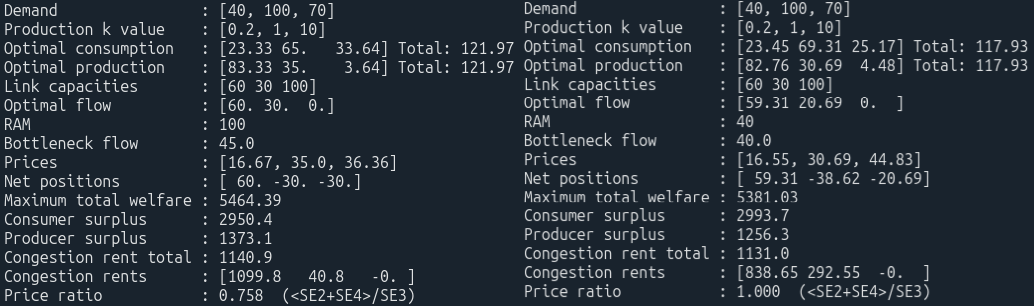
Dessa utbuds och efterfrågekurvor är ju bara väldigt grova approximationer av de verkliga, men är satta så att de ska ge en rimlig prisbild i resp område. Nu kan vi se lite bättre vad som händer rent fysiskt i modellen. Utan RAM begränsning (till vänster) får vi nettopositioner som avspeglar begränsningarna mellan elprisområden. Dvs SE3 importerar så mycket det går från SE2, och SE4 importerar så mycket det går från SE3. SE3 och SE4 ligger nära varandra i pris.
Till höger går RAM flaskhalsen i SE3 aktiv (dvs flödet genom Lab begränsas till RAM värdet, 40 i det här fallet). Flödena över L23 (59.31) och L34 (20.69) ligger nu under gränserna 60 resp 30 så hela prisbilden styrs nu av flaskhalsen i SE3, och vi ser att kvoten blir exakt 1. Dessvärre betyder det också att prisskillnaderna nu ökar mellan SE3 och SE4. Mer av elen från SE2 “fastnar” i SE3 pga flaskhalsen vilket medför att priset blir lägre i SE3 och högre i SE4.
Obserera att utfallen ovan kommer från en ren välfärdsoptimering med hänsyn till begränsningarna. Vi använder inte explicit formeln för prisjustering pga av flaskhals enligt ovan, utan detta utfall är en konsekvens av optimeringen (se “teori-kollen” i appendix nedan).
I den översta figuren till höger finns ett histogram över priskvoterna när man i simuleringen slumpmässigt ändrar efterfrågan i SE3 och SE4, samt ändrar RAM i ett intervall runt 40. Det som är intressant att se är att de kvalitativt visar på liknande egenskaper, dvs en kontinuerlig fördelning mellan ett minvärde (0.5 med statistik från elprisdata, och 0.7 i det simulerade fallet), upp till en peak nära 1, och med enstaka utfall över 1. Dessutom ligger även i simuleringen ungefär hälften av utfallen i peaken runt 1, som i det verkliga fallet. Om detta är en slump eller inte, vet jag inte.
Sen kan man ju undra om SE3/SE4 gränsen är på rätt ställe, eller vad det är för vits att ha en gräns om flaskhalsen “hoppar runt”?
Fenomenologiskt
En annan aspekt av den här flaskhalsen är att den i princip alltid är associerad med ett högt flöde på FennoSkan linken mellan SE3 och FI. Och ofta “mot prisgradienten” dvs el flödar från SE3 till FI även om priset är lägre i FI. Den intuitiva förklaringen skulle vara att flaskhalsen helt enkelt tvingar ett överskott av el från SE2 och östra SE3 att flöda över till FI, som elektriskt är nära kopplat till dessa områden, nästan oberoende av pris. Detta flöde minskar priset i FI, speciellt om t ex länken mellan FI och Estland är begränsande och överskottet fastnar i Finland. Om vi hypotetiskt tänker att vi skulle stänga av SE3 -> FI flödet skulle detta inte förbättra situationen nämnvärt i Sverige, troligen skulle bara exporten SE2 -> SE3 minska, priserna i SE3/SE4 vara i stort oförändrade och priserna i SE2 bli ännu lägre än vad de redan är. (Alternativet att i stället flöda till Norge (NO1) finns inte då NO1 elektriskt, med avseende på den här flaskhalsen, är mer kopplat till SE3/SE4).
Ur systemsynpunkt skulle en sån “blockering” av FennoSkan fytta konsumentöverkottet från Finland till SE2. Men ur välfärdssynpunkt är det bättre att sänka priset i Finland än att ytterligare sänka priset i SE2.
Appendix: Teori-koll
Skuggpriset μ för begränsningen Lab kan tas fram på två sätt
- Genom “formeln” ovan som säger att skillnaden mellan priserna i SE4 och SE2 är lika med skuggpriset
- Genom definitionen på skuggpris, hur mycket ändrar sig “total welfare” när man ändrar begränsningen en enhet
Modellen har data för att beräkna på båda sätten:
- SE4 – SE2 priser vid RAM = 40 finns i datan ovan: 44.83 – 16.55 = 28.28
- Gör två beräkningar runt RAM 40 och inspektera “Total welfare (TW)”
TW(RAM = 40.5) = 5395.06
TW(RAM = 39.5) = 5366.78
Skillnaden (5395.06 – 5366.78) / (40.5 – 39.5) blir… 28.28!
Teori och praktik i skön förening!
Metod 1: Enligt μ = P(SE4) – P(SE2)
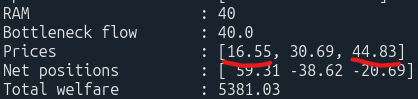
Metod 2: μ = dTW/dRAM