Bengt J. Olsson
Twitter: @bengtxyz
LinkedIn: beos
In earlier posts, we explored a two-zone and a three-zone electricity market, each with different demand and supply curves. By allowing electricity to flow from low-price zones to high-price zones, total welfare was maximized. However, these models assumed perfect flexibility, ignoring the physical constraints of the power network, instead flows were determined solely by economic optimization.
In this post, we revisit the three-zone market and examine how the results change when physical realities, such as network impedances, are taken into account. We also introduce a new concept: a zone-internal congestion point (a.k.a. a “CNEC”). This internal bottleneck can lead to price splitting, and also un-intuitive flows, even when there’s no congestion between zones.
An interesting observation from the three-zone model is that while net positions are uniquely determined by economic optimization, the flows between zones are not. The net position of a zone can be interpreted in two equivalent ways:
- The difference between supply and demand within the zone
- The net export: the sum of flows out of the zone minus the sum of flows into the zone
As long as the net positions of the zones remain the same, there are infinitely many possible flow configurations between them—unless a congestion occurs. (See the previous post on the three-zone model for concrete examples of this.)
In practice, however, only one set of flows will occur. This set is determined by economic optimization, but subject to physical constraints of the power network. Let’s take a closer look at those constraints.
Introducing Internal Congestion
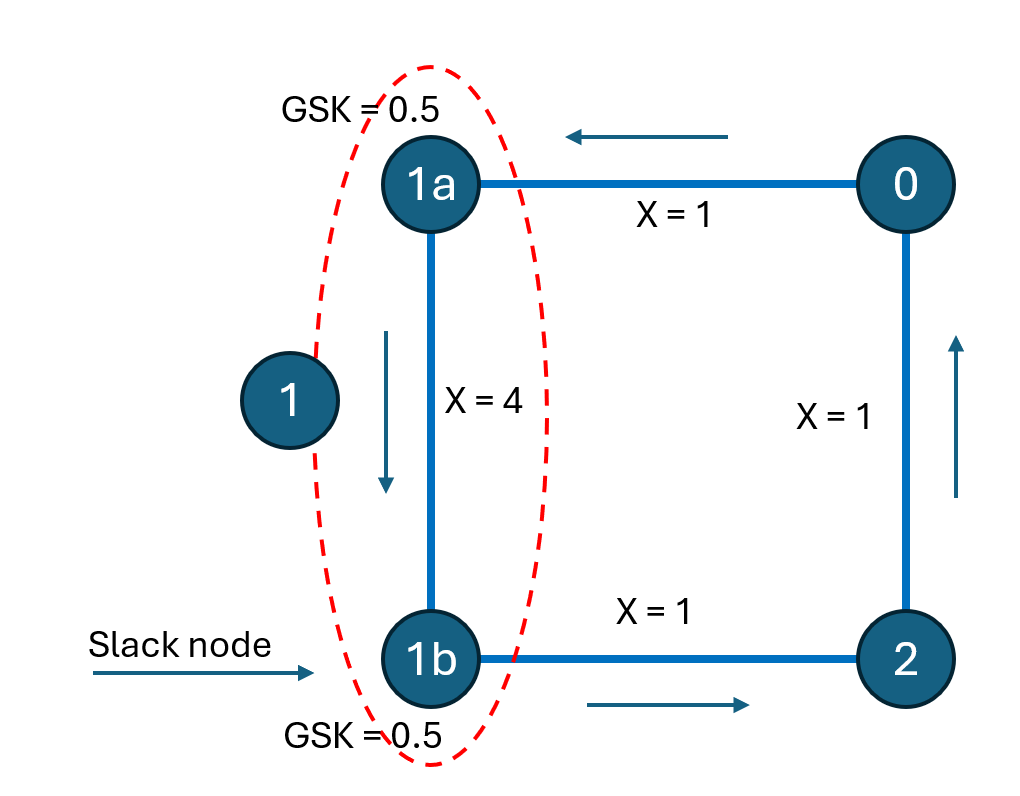
To account for physical network constraints, we revisit the three-zone market but introduce more detail: zone 1 is now represented by two sub-nodes, 1a and 1b, connected by an internal link, which may become congested.
PTDF Matrix and Flow Allocation
In power systems, flows across the network are governed by the Power Transfer Distribution Factor (PTDF) matrix. This matrix relates injections at nodes to flows on links in a linearized model.
- Each row in the PTDF matrix corresponds to a link in the network
- Each column corresponds to a node
- Entry PTDFij describes how much flow is induced on link i by injecting 1 MW at node j (with the slack node compensating)
The total flow on any link is then the sum of the effects of injections at all nodes, weighted by their respective PTDF values. This follows directly from the principle of superposition in linear systems.
In our case, we use the following assumptions:
- All external links (between zones) have a reactance of 1 ohm
- The internal link within zone 1 has a reactance of 4 ohm
- Node 1b is selected as the slack node
With these parameters, we can compute the full PTDF matrix for the four-node network. (For a detailed method, refer to the earlier post on PTDF calculation.)
Full PTDF Matrix
The full PTDF matrix describes how injections at each node (0, 1a, 1b, 2; 1b selected as slack node) affect flows on each link (including the internal one). Here’s the table governed from the impedances of the full network:
| PTDF matrix. Zone/Node: Link: | 0 | 1a | 1b | 2 |
| 0 | 2/7 | -4/7 | 0 | 1/7 |
| Internal | 2/7 | 3/7 | 0 | 1/7 |
| 1 | -5/7 | -4/7 | 0 | -6/7 |
| 2 | -5/7 | -4/7 | 0 | 1/7 |
Aggregating to Zones Using GSK
To reduce the model back to three zones, we consolidate nodes 1a and 1b into a single zone (zone 1). This requires applying a Generation Shift Key (GSK) to describe how internal nodes contribute to the zone’s net position.
Here, both 1a and 1b are assigned a GSK of 0.5, meaning they each account for half of zone 1’s net injection.
Since node 1b (the slack) contributes zero to all flows, only the 1a values affect the result, and they are halved. The consolidated PTDF matrix (zones 0, 1, 2 vs. links) becomes:
| PTDF matrix. Zone: Link: | 0 | 1 | 2 |
| 0 | 2/7 | -2/7 | 1/7 |
| 1 | -5/7 | -2/7 | -6/7 |
| 2 | -5/7 | -2/7 | 1/7 |
Internal Constraint in Zone 1
To express the internal constraint on the link between 1a and 1b (within zone 1) in terms of zone net positions, we use the following formula:
Flow on internal link:
(2⁄7) × NP0 + (3⁄14) × NP1 + (1⁄7) × NP2
PTDFs comes from the “Internal” row in the full PTDF matrix. Note the factor 0.5 from the GSK for node 1a, imposed on the second term. To ensure this internal link does not exceed its capacity, we impose the constraint:
(2⁄7) × NP0 + (3⁄14) × NP1 + (1⁄7) × NP2 ≤ RAM
Here:
- NPi is the net position of zone i
- RAM is the Remaining Available Margin of the internal link, i.e. its maximum allowable flow
Simulating the three-zone model with constrained flows
The three-zone model from the earlier blog post has now been extended as described above, while keeping the original supply and demand curves to allow for a clear, head-to-head comparison. The key difference is that we now maximize welfare subject to an additional constraint: the internal link must not become overloaded.
Let’s explore how this affects the outcome under different scenarios.
No congestion anywhere
The first scenario considers a case with no congestion. In other words, both the RAM of the internal link and the capacity C of the interconnecting links are sufficiently large to avoid any bottlenecks. This allows the system to operate purely according to economic optimization.
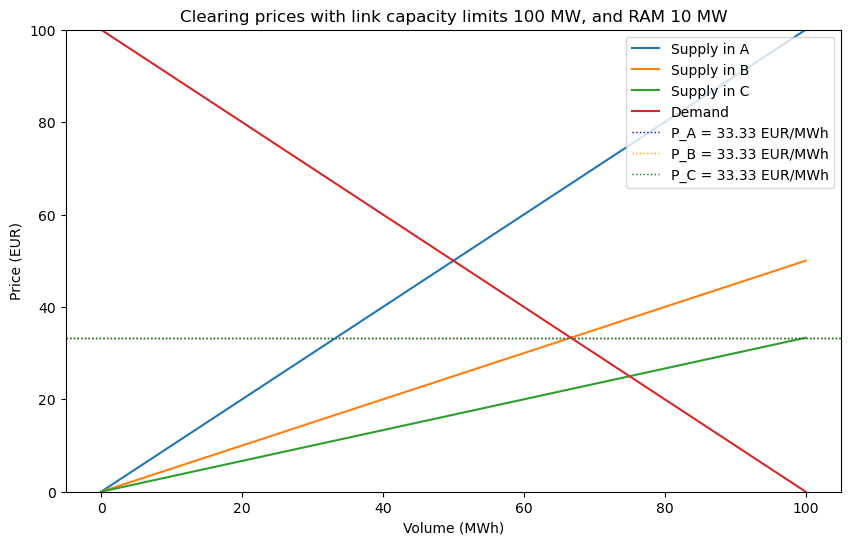
Production k value : [1, 0.5, 0.33]
Link capacities : [100 100 100]
Optimal consumption : [66.67 66.67 66.67] Total: 200.0
Optimal production : [ 33.33 66.67 100. ] Total: 200.0
Optimal flow : [-4.76 -4.76 28.57]
-RAM : -10
Bottleneck flow : -4.76
Prices : [33.33, 33.33, 33.33]
Net positions : [-33.33 0. 33.33]
Maximum total welfare : 10000.0
Consumer surplus : 6666.7
Producer surplus : 3333.3
Congestion rent : -0.0
The results in this scenario are identical to those of the previous three-zone model, with one important exception: the flows. Net positions, welfare, production, consumption and prices remain unchanged, but the actual power flows differ because they are now determined by the PTDF matrix.
We observe that the largest flow occurs directly from the low-cost zone 2 to the high-cost zone 0. Due to the higher impedance in zone 1, less power is routed through that path.
Congestion on interconnect links
If we now reintroduce the capacity limit of 16.67 (as used in the original three-zone model), we observe that it is no longer possible to transfer enough power from zone 2 to zone 0 to fully equalize the prices. The PTDF determined flow is restricted by the capacity constraint C, resulting in a price difference between the zones.
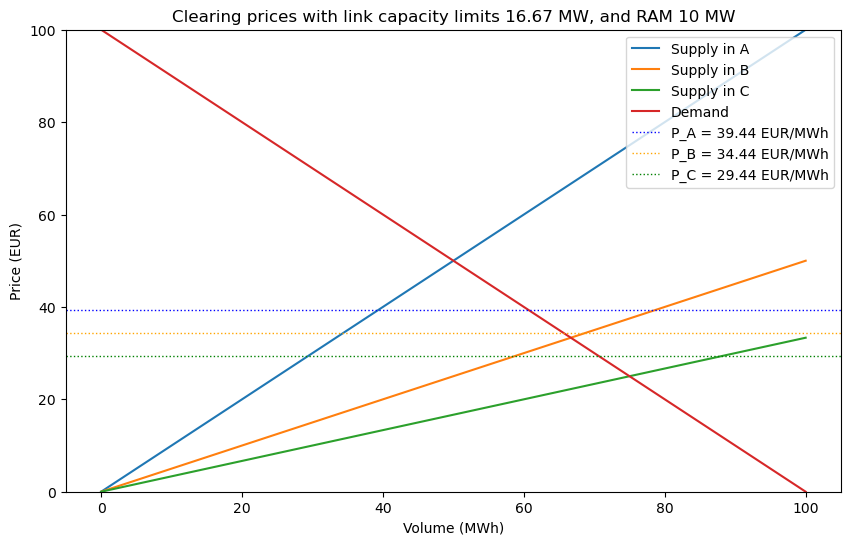
Production k value : [1, 0.5, 0.33]
Link capacities : [16.67 16.67 16.67]
Optimal consumption : [60.56 65.56 70.56] Total: 196.67
Optimal production : [39.44 68.89 88.33] Total: 196.67
Optimal flow : [-4.44 -1.11 16.67]
-RAM : -10
Bottleneck flow : -2.78
Prices : [39.44, 34.44, 29.44]
Net positions : [-21.11 3.33 17.78]
Maximum total welfare : 9930.56
Consumer surplus : 6471.3
Producer surplus : 3264.8
Congestion rent : 194.4
Link 2, which connects nodes 2 and 0, becomes the limiting factor in this case. This illustrates the direct impact of the network’s physical properties, such as line impedances, on how power can flow through the system.
Importantly, the internal congestion within zone 1 is not limiting in this scenario, it remains non-binding despite being part of the model.
Congestion on zone 1 internal link
Now, let’s introduce a congestion on the internal link within zone 1 by setting the RAM to 4 MW, while keeping the interconnecting links unconstrained. As shown in the table, the flow on the internal link is now limited to 4 MW, making it a binding constraint and the new bottleneck in the system.
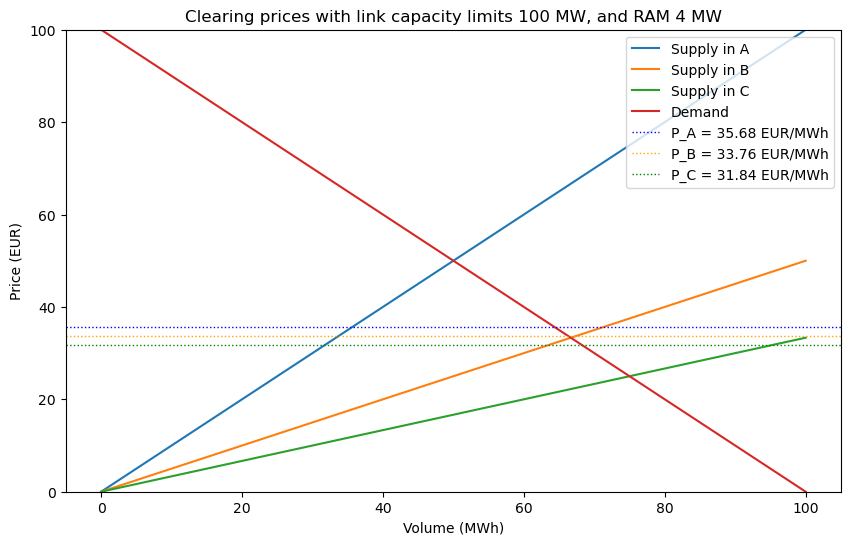
Production k value : [1, 0.5, 0.33]
Link capacities : [100 100 100]
Optimal consumption : [64.32 66.24 68.16] Total: 198.72
Optimal production : [35.68 67.52 95.52] Total: 198.72
Optimal flow : [-4.64 -3.36 24. ]
-RAM : -4
Bottleneck flow : -4.0
Prices : [35.68, 33.76, 31.84]
Net positions : [-28.64 1.28 27.36]
Maximum total welfare : 9989.76
Consumer surplus : 6585.3
Producer surplus : 3296.9
Congestion rent : 107.5
This leads to an interesting phenomenon: price splitting occurs between the zones even though the interconnecting links are not congested. The internal bottleneck within zone 1 alone is enough to disrupt price convergence across the system.
The shadow price of the RAM congestion can be calculated “backwards” since we know the total congestion rent which is 107.5. In formal theory the shadow price (when the constraint is binding) equals the congestion rent divided by the RAM. In this case λ = RAM/CR = 107.5/4 = 26.875. We can cross-check this value by looking at the price differences. For example PA – PB = λ*(PTDFA – PTDFB) = > PA = 33.76 + 26.875*( 2/7 – 3/14) = 33.76 + 26.875/14 = 35.68 which is exactly the price in zone A above.
More congestion on internal link
Let’s take it a step further and decrease the RAM to just 2 MW. Now something even more interesting happens: the internal congestion in zone 1 becomes even more dominant, significantly reshaping the flow pattern and price formation across the entire network.
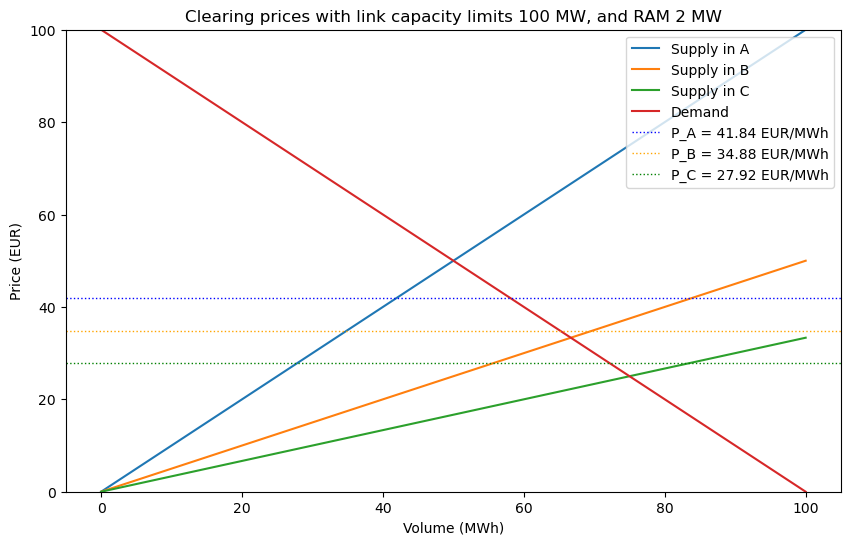
Production k value : [1, 0.5, 0.33]
Link capacities : [100 100 100]
Optimal consumption : [58.16 65.12 72.08] Total: 195.36
Optimal production : [41.84 69.76 83.76] Total: 195.36
Optimal flow : [-4.32 0.32 12. ]
-RAM : -2
Bottleneck flow : -2.0
Prices : [41.84, 34.88, 27.92]
Net positions : [-16.32 4.64 11.68]
Maximum total welfare : 9865.44
Consumer surplus : 6409.4
Producer surplus : 3261.2
Congestion rent total : 194.9
Congestion rents : [ 30.07 -2.23 167.04]
The most notable feature here is that the increased congestion in the “middle” zone B decreases the absolute values of the A and C zones significantly (A imports less and C exports less), with a consequent higher price difference between all zones.
Also we now see a flow from the more expensive zone 1 to the cheaper zone 2. Since the cheapest zone 2 cannot send enough power through zone 1 to zone 0, due to the internal congestion in zone 1, it becomes more effective overall to export more from zone 1 and reroute the power through zone 2 to the expensive zone 0.
Once again, this is a result of economic optimization (welfare maximization) constrained by physical limitations represented by the PTDF matrix. The non-intuitive flow pattern is also accompanied by a negative congestion rent.
Note! The non-intuitive flows are not necessarily caused by internal binding constraints. Also border capacity constraints (with no internal constraints) can incur non-intuitive flows because of how the PTDF matrix steers the power flows. That is, the economically most viable path may not be possible, since physics dictates other flows, through the PTDF matrix.
The shadow price λ = CR/RAM in this case is 194.9/2 = 97.5. Thus when we shrunk the RAM from 4 to 2 the shadow price increased almost four-fold.
Summary
The economic optimization of the three-zone market model from the previous blog post has here been extended to include physical constraints based on network impedances. This introduces several important features:
- The PTDF matrix, derived from network impedances, effectively “locks in” the previously indeterminate flows, making them physically consistent.
- Most power flows from low-cost zones to high-cost zones via the paths of least impedance.
- An internal congestion within a zone can lead to price differences between zones, even when the inter-zonal links are uncongested.
- When the RAM on an internal link is sufficiently small, non-intuitive flow patterns can emerge as the system reconfigures itself to maximize total welfare within the physical limits.
Additional
The algorithm used here is to maximize the total welfare of the system
Welfare = Consumer Utility – Producer Cost (U – C)
subject to the following constraints
- Sum of net positions equal to zero (market balance)
- Zone 1 internal link flow < RAM (CNEC constraint)
- Interconnect link flows < C (interlink constraints)
Welfare can be decomposed as CS + PS + CI, when prices and flows are established.
The independent variables (x) are the demand and supply in each zone. Net position is given as supply – demand. The constraints are formulated as
cons = [
{'type': 'eq', 'fun': lambda x: np.sum(netpos(x))}, # sum n = 0 (market balance)
{'type': 'ineq', 'fun': lambda x: RAM - abs(np.dot(ptdf_intern, netpos(x)))}, # Zone 1 internal link constraint, ptdf_intern = [2/7, 3/14, 1/7]
{'type': 'ineq', 'fun': lambda x: C - max(abs(flows(netpos(x))))}, # Interconnect link constraints
]
The solver used is scipy.optimize.minimize. Since this solver only handles the primal problem, it cannot directly produce shadow prices related to the constraints. However, when there is only one congestion we can find its shadow price “backwards” as seen in the examples above.
added 2025-12-31
Added a blog Effects of an Internal Constraint in Flow-Based Welfare Maximization based on the model above. It looks at the system behavior with only one binding constraint, the internal in Zone 1. (Interconnect links are given a high capacity of C = 100 and are hence unconstrained). When RAM is varied from zero to its unbinding limit, the impact on prices and shadow price is plotted as well as impact on Welfare and particularly (CS+PS) and CI respectively.
