Bengt J. Olsson
Twitter: @bengtxyz
In an article in the Finnish daily newspaper Helsingen Sanomat, a concept for producing a guaranteed base load power, corresponding to a large nuclear reactor, is presented. Unfortunately there is no reference to a report, but the context seems rather clear from the summary table:

So the basic assumption is that with about 7 GW of wind power, balanced by hydrogen produced from 1.93 GW of electrolyzer capacity when the wind power is above the base load level of 1.6 GW. The produced hydrogen is subsequently burnt as fuel in a hydrogen gas turbine when the power delivery from the wind power is less than 1.6 GW.
This all sounds very nice, that we can create this “plannable” base load power from renewable energy sources with some aid from electrolyzers and hydrogen gas turbines. Without expensive nuclear plants.
All to a much lower price per MWh also. However, in this post we will not consider the cost per MWh aspect. Instead we will focus on another aspect that is only incidentally mentioned, but is crucial to the success of such a concept: the storage aspect.
Since wind power dispatch is weather dependent and varies, the produced hydrogen must be stored while waiting to be consumed. But the size of this storage is not discussed at all. But here is where our balance model comes in handy! We modify the balance model to fit the Wärtsilä base power production scenario as follows.
We use (the by now famous…) Swedish wind power statistics from 2020-2021 and scales it so that it produces yearly what we expect to be the output from a 7.24 GW of installed wind turbines. With 30% capacity factor we get 19.5 TWh per year. This is the target value we will scale the our wind power sources to generate.
Then we set the “demand” to 1.6 GW constantly. The model will then use the wind power above 1.6 GW to produce hydrogen and add this hydrogen to a store. When the wind power is below 1.6 GW it will conversely withdraw hydrogen from the store in order to consume it as fuel for the power producing hydrogen turbine. Note that the withdrawal rate will be the needed turbine power divided by 40%. The 40% comes from the assumed power-to-gas-power efficiency. That is for 1 GWh input to the electrolyzers we will have only 0.4 GWh out from the (combined cycle) gas turbine. Hence if we want 1 GWh out we consume what corresponds to 2.5 GWh in to the system.
BTW the 250 MW battery is totally excluded from this model. It would have a storage capacity around 1 GWh which is insignificant for energy storage in this context as will be seen. In a real world case it would be useful to provide inertia and frequency services, but not for the energy storage we focus on here.
Infinite store
Let’s first look at a infinitely large store and see how the power dispatch and store levels behave.
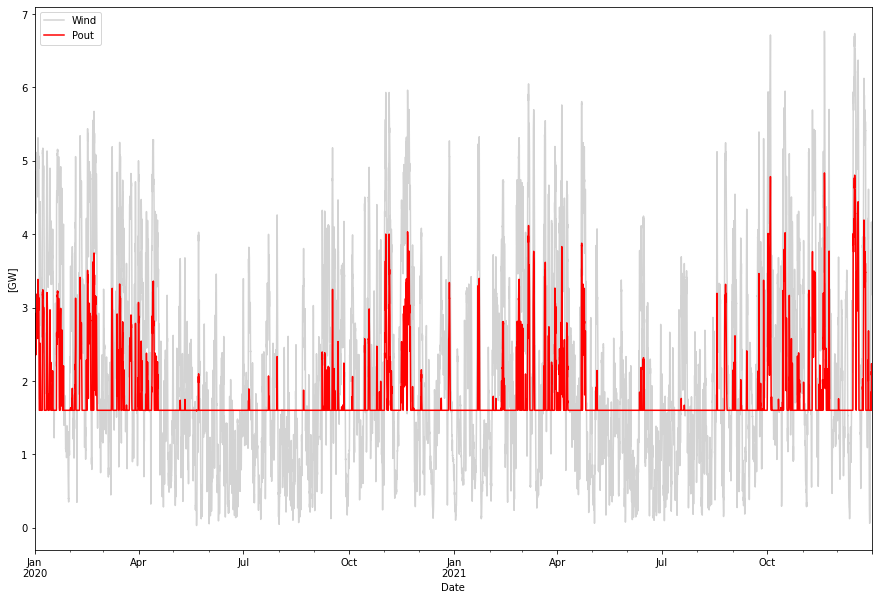
As we can see we now have at least base load delivery at 1.6 GW and even more. In fact the numbers are
Supplied power per year: 19.54 TWh Delivered power per year 15.62 TWh Baseline power per year: 14.04 TWh
The supplied power per year is the produced wind power. Baseline power is the 1.6 GW yearly energy. Actually delivered energy is 15.62 TWh. The lost energy is essentially the efficiency loss in the power-gas-power cycle (plus that we have a positive net balance of hydrogen in the store by the end of the second year, see below).
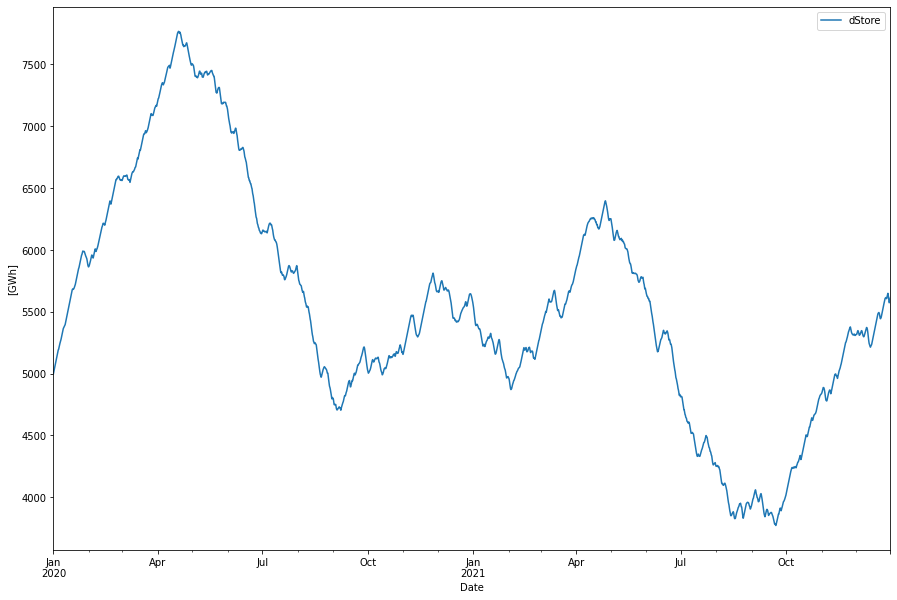
1 TWh store
So with the infinite size store it works like intended. But let’s take a look at a future 1 TWh store. Such a store does not yet exist but could for example be 10 of the Lined Rock Caverns (LRC) that the HYBRIT green steel project in Sweden are considering. Each such store is a around 120.000 cubic meters cavern deep down in the mountain ground, lined with a sheet of steel (made to withstand the embrittlement that the hydrogen gas impose on the steel). One such LRC can house about 100 GWh of hydrogen at 200 bars pressure. Hence 10 of these LRCs could sum up to a 1 TWh store.
Here is the power dispatch in this sceanrio.
But what happens here? After longer streaks of low wind the store is empty and cannot supply base load power any more. Interestingly this scenario delivers more energy in total than with the infinite store, 16.8 instead of 15.6 TWh:
Supplied power per year: 19.54 TWh Delivered power per year 16.80 TWh Baseline power per year: 14.04 TWh
This is because when the store is full, wind power that should have been used to produce more hydrogen is dispatched into the network with a higher efficiency than if going through the power-gas-power cycle. But instead we cannot provide base load power.
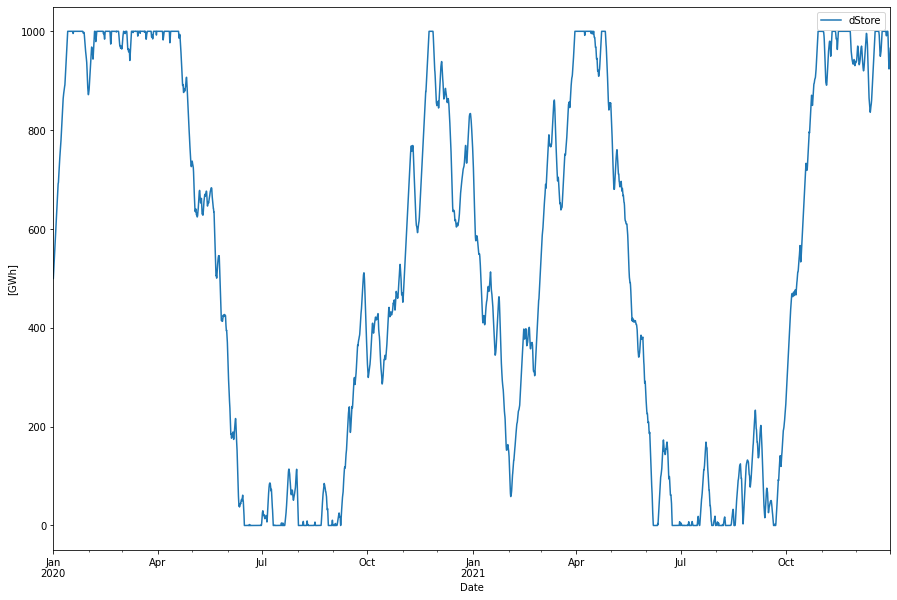
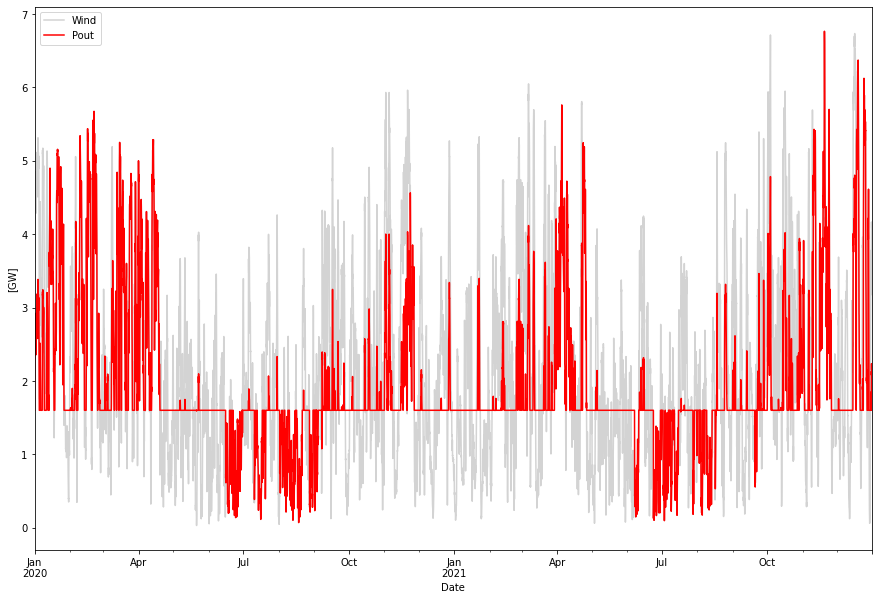
Real life store
Finally lets look at a real life store which happens to be the “Skallen” natural gas store in Sweden. It is unique in Sweden and also presently the largest LRC in the world. Given that it could be converted to a hydrogen store it could keep about 25 GWh of hydrogen. This is how it would perform.
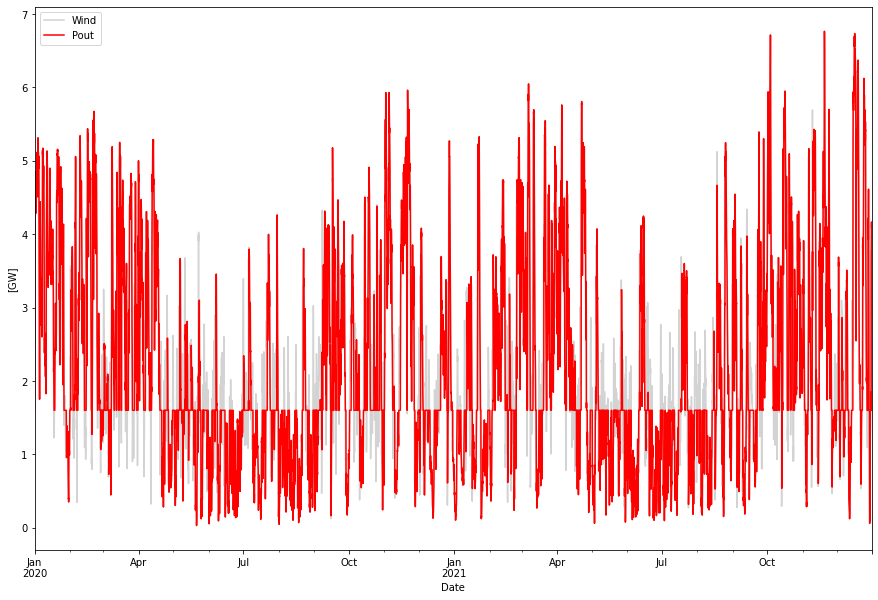
Supplied power per year: 19.54 TWh Delivered power per year 18.82 TWh Baseline power per year: 14.04 TWh
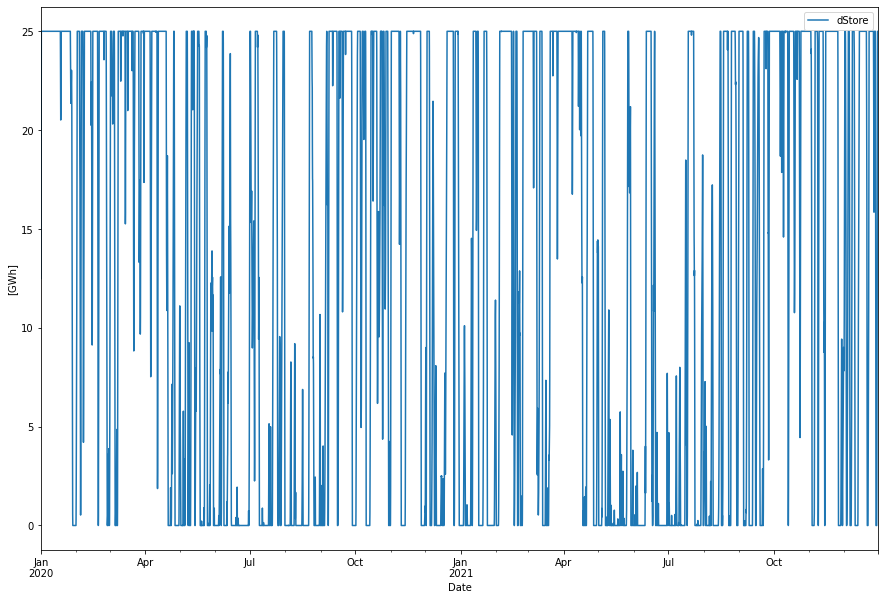
This store does little to help smooth out the variations in the wind power.
Conclusions
While the wind (or sun) power plus balancing hydrogen power production sounds as an attractive proposition to deliver base load power, the enormous amount of hydrogen storage much be considered. If no salt caverns or aquifers are available (and they aren’t in Sweden or Finland), Lined Rock Caverns are the only viable alternatives.
But from the infinite store example we can see that in order to deliver base load power, 1.6 GW, at all times we would need a 4+ TWh store. Or 160+ of the unique “Skallen” store which is the largest LRC in the world presently.
It is not easy to calculate the cost of these stores since they have never been built, but they would presumably weigh down the business case for this solution.
Update
Revisited this case here, one and a half year later 2024-06-02.
